
Si no tienes idea sobre el tema o has escuchado algo apenas, pero quieres entender qué es esto de las tasas de interés, quédate tranquilo que en este artículo te lo explico todo.
Imagínate que tu amigo un día te pide prestados $1.000 y tú muy desinteresadamente le prestas y le dices que te los pague en 6 meses. Muy puntualmente después de ese tiempo te devuelve los $1.000, ¡genial! Te devolvió todo, seguro se lo vuelves a prestar, no te devolvió menos dinero de lo que le prestaste por lo tanto no perdiste dinero ¿verdad? ¡Pues no! déjame te digo que has hecho un mal negocio, el dinero cambia de valor en el tiempo y estás perdiendo dinero.
Vamos poco a poco para entender qué es esto de la tasa de interés. Empecemos con una escala más amplia, supongamos que no son 6 meses si no 30 años. ¿Recuerdas qué podías comprar hace 30 años con $1.000? Más o menos el doble de cosas de lo que podrías comprar ahora con esa misma cantidad. Esto se debe a que los precios normalmente están incrementando poco a poco, año tras año, esto se conoce como inflación y hace que el dinero que tienes en un momento dado pierda “valor” en el futuro.
Ahora conectémoslo con el préstamo que hiciste a tu amigo, tú le diste $1.000 hace 30 años, pero a pesar de que él te devuelve íntegramente todos esos $1.000, tú pierdes porque solamente podrás adquirir más o menos la mitad de cosas que hubieras podido adquirir hace 30 años.
Si hubieras pedido a tu amigo que te pague porcentaje adicional del 3.2% de los $1.000 cada año para compensar la inflación, lograrías tener exactamente el mismo poder adquisitivo que hace 30 años.
En otras palabras, el monto acumulado total que recibirías sería $1960 y con eso puedes adquirir hoy las mismas cosas que podías adquirir hace 30 años con $1.000.
Este porcentaje de 3.2% que equivale a $32 cada año ($1.000 multiplicado por 3.2%), ilustra muy bien el caso de una tasa de interés simple, es el porcentaje aplicado a una cantidad fija inicial. Ese valor inicial de $1.000 es conocido como capital. Y los intereses en cada año son fijos, por un valor de $32.
Vamos más allá. Al momento de prestar esos $1.000 dólares a tu amigo, probablemente había algo más en lo que podías usar ese dinero. Como pagarte un viaje y satisfacer un gusto o utilizarlo para comprar un horno, hacer pan y venderlo a tus vecinos, lo que te produciría ganancias.
En ambos casos estás obteniendo una ganancia, en el primero no monetaria y el segundo sí. Al decidir entre estas opciones, necesitas saber cuál es mejor, calculando con cuál ganarías más, esa diferencia se conoce como costo de oportunidad y la tasa de interés debe representar para ti un valor mejor que esa ganancia que dejarías de percibir con el horno o el viaje al prestar dinero a tu amigo.
Calcular monetariamente esas ganancias a nivel de satisfacción personal o de un proyecto más complejo va a ser muy subjetivo y difícil por lo que hay referencias de tasas de interés que utilizan los bancos y otras entidades financieras para determinar cuáles son las tasas que van a cobrar por sus préstamos. Y muchas veces son determinadas simplemente por la oferta y demanda de dinero y otras variables económicas.
Así, tú también podrías utilizar las tasas referenciales para saber cuánto deberías cobrar a tu amigo en intereses. Por supuesto es tu decisión y no es una obligación cobrar intereses, el ejemplo es simplemente para ilustrar la idea.q
Entonces, ¿Qué es una tasa de interés?
Una tasa de interés es el porcentaje adicional que es aplica en un período de tiempo dado a un monto de dinero definido para ese período. En concepto, representa el valor del dinero en el tiempo.
Pero, ¿no es muy arriesgado prestar dinero a tanto tiempo?
En efecto, hay que tener en cuenta que prestar dinero conlleva cierto riesgo de que no te paguen. Mientras mayor sea el plazo, el riesgo de no pago es mayor. Por lo tanto, podrías decidir prestarle a tu amigo solamente a un año y renovar el préstamo un año más en caso de que lo pague puntualmente y así sucesivamente hasta 30 años. O hacerlo de forma mensual y renovarlo cada mes.
Entonces, imagina que en ese préstamo de $1.000 que hiciste a tu amigo, el primer año te paga $32 en intereses y le renuevas los $1.000 otro año. Al siguiente año se generan nuevamente $32 de intereses y así hasta el final, en forma de interés simple, pero ¿Qué pasa si tu amigo prefiere no pagarte el interés cada año y guardárselo para acumularlo y pagarte todo al final de los 30 años?
Ese interés ahora es un dinero que estás dejando de recibir y tiene un costo de oportunidad, ¿Qué deberías hacer? Aquí entra en juego la tasa de interés compuesta, veámoslo.
¿Qué es una tasa de interés compuesta?
En nuestro ejemplo, la tasa de interés de 3.2% se calculará el segundo año en base a $1.032 porque ahora ese es el valor del capital (los intereses de $32 se suman al capital inicial de $1.000) y ahora los intereses ya no serán $32 si no $33.02 ($1032 multiplicado por la tasa de 3.2%) y si sigues renovando el capital + intereses cada año, ese valor va incrementando cada año de forma exponencial. De esta forma:
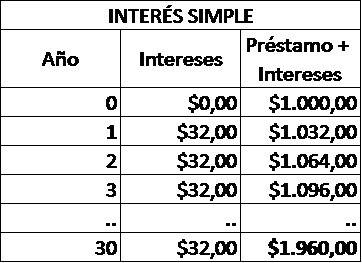
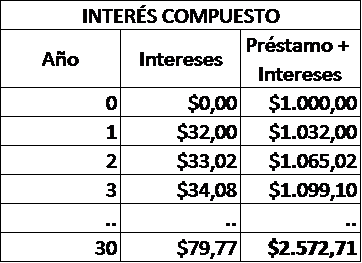
Como puedes ver, los primeros años no hay mucha diferencia, especialmente con una tasa de interés baja, pero al año 30, el valor acumulado es ampliamente mayor en el caso del interés compuesto.
Seguramente vas a querer definir un límite en esas renovaciones, que en nuestro caso es 30 años y finalmente cobrarlo en ese momento para no volver a renovarlo. Muchos préstamos, por simplicidad, definen un plazo final para el pago de todo el préstamo, pero con capitalización de los intereses cada cierto tiempo, el cobro y renovación es solamente un hecho cuya operación no se lleva a cabo realmente entre las partes en cada período. En nuestro ejemplo los períodos son anuales, pero también puede ser mensual, trimestral, incluso diario.
En definitiva, ¿Qué es el interés compuesto?
El interés compuesto funciona igual que el interés simple y también representa el valor del dinero en el tiempo. Es un porcentaje adicional que es aplica en un período de tiempo dado a un monto de dinero definido para ese período. La diferencia con el interés simple es que se calcula adicionalmente el interés sobre el interés no pagado para cada período que transcurre. Tras un período, ese interés generado ya es considerado parte del capital.
Unos datos finales…
En la antigüedad se generaba una confusión. La práctica de cobrar intereses sobre intereses era considerada usurera e ilegal, incluso solo el hecho de cobrar intereses lo era. Pero ten en cuenta lo que hablamos sobre el valor del dinero en el tiempo y el costo de oportunidad, por lo que ahora es legal y lógico utilizar el interés compuesto en las operaciones financieras.
La tasa de interés compuesta se utiliza en millones de operaciones todos los días en el mercado financiero. De hecho, ha favorecido a que muchas personas puedan incrementar su patrimonio a través de inversiones en diferentes medios y lograr una buena salud financiera.
En Ecuador existen algunos medios formales para invertir y aventajarse de esta maravillosa tasa de interés compuesta. Una gran alternativa es el mercado de valores, que es accesible a cualquier persona y es recomendable invertir desde $1.000.
Hay la creencia equivocada de que la Bolsa de Valores es riesgosa, cuando todo depende de recibir una buena asesoría. Además, no solo se puede invertir en acciones, hay otros productos generalmente menos riesgosos y las tasas de interés casi siempre son más altas que las de nuestro ejemplo e incluso más altas que medios tradicionales como la banca. ¿Te imaginas el valor final de una inversión con tasas de interés más altas que la de nuestro ejemplo?
Nota: Este artículo fue publicado originalmente el 1 de julio de 2021 y actualizado con información más relevante en agosto de 2021.


Comentarios recientes